Pentru generarea unui fractal (acest lucru se face printr-un şir vast de operaţii) se pot folosi trei tehnici. Trebuie remarcat că operaţiile din procesul de generare a unui fractal sunt extrem de simple (adunare şi înmulţire). Având în vedere acest lucru, ar trebui să ne punem întrebarea:”de ce nu au fost fractalii observaţi mai devreme de a doua jumătate a secolului XX?”
Răspunsul este dezarmant de simplu – pentru că un fractal este alcatuit dintr-o infinitate de puncte ce reprezintă coordonatele unor numere complexe din plan. Pentru a figura aceste puncte, operaţiile de adunare şi înmulţire trebuie efectuate de un număr de ori de ordinul milioanelor şi zecilor de milioane. Cu cât numărul de operaţii este mai mare, cu atât gradul de detaliu al fractalului respectiv este mai mare. Cu ajutorul computerelor, oamenii de ştiinţă au reuşit să vizualizeze fractalii şi să îi genereze într-un ritm imposibil de susţinut la nivel uman.
Prima din tehnicile folosite pentru generarea unui fractal sunt sistemele de funcţii ce se iterează. Iterarea face ca o valoare obţinută în urma calculului unei funcţii să devină noua valoare a parametrului sau parametrilor funcţiei respective. Ca exemple de fractali ce se generează cu ajutorul acestei metode remarcăm praful lui Cantor, curba Peano, curba lui Harter-Heighway, ş.a. O altă tehnică uzitată în procesul de generare a fractalilor este aşa-numita „escape time technique”. Aceasta se bazează pe o relaţie de recurenţă în fiecare punct din spaţiu. Exemple de astfel de fractali sunt : ansamblul lui Mandelbrot(1) , fractalul corabie în flăcări(2) şi fractal.
A treia categorie de fractali sunt reprezentaţi de fractalii aleatorii. Generaţi mai degrabă stochastic decât deterministic, aceşti fractali se regăsesc sub forma peisajelor fractale şi a “fractalilor copaci.
Fractalii în natură şi aplicaţiile acestora
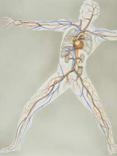
Structurile fractale sunt prezente atât în alcătuirea organismului uman, cât şi în tot ceea ce se află în jurul nostru de la fulgi de zăpadă, forme de relief, creierul uman, până la componente ale lumii vegetale (ferigă, aloe). Un ochi „antrenat”, spunea Barnsley , poate observa o structură fractală în aproape orice element al lumii înconjurătoare. Principiul părţii asemănătoare cu întregul (principiul autoasemănării) este cuprins şi realizat aproximativ în natură. Unii fractali suferă schimbări continue ca formaţiunile noroase sau focurile licărind, iar alţii precum sistemul vascular uman sau copacii reţin structura pe care au dezvolat-o în evoluţia lor. Până şi moleculele de oxigen şi ADN reprezintă fractali, iar şirul de exemple nu se termină aici.
In informatică, fractalii au revoluţionat tehnica de comprimare a imaginilor. Prin transformarea lor (a imaginilor) în fractali, Barnsley a descoperit o tehnică prin care se pot comprima imagini foarte mari în coduri foarte mici, obţinându-se un raport de comprimare de peste zece mii la unu. Ceea ce este şi mai impresionant însă este faptul că atunci când se măresc aceste imagini, ele îşi păstrează gradul de detaliu la infinit, un lucru oarecum neobişnuit la imaginile stocate clasic, la care la o mărire nu foarte puternică se instalează deja neclaritatea, devenind imagini pixelate.
Pentru a înţelege mai bine rolul computerelor în generarea fractalilor şi în aplicaţiile legate de aceştia vă voi expune modalitatea care se aplica în tehnica de compresie a imaginilor prin găsirea unei funcţii fractale care să poată fi folosită pentru micşorarea acestora înainte de inventarea unei modalităţi prin care computerele să poată să determine singure aceste funcţii. Sute de ore de muncă erau necesare pentru identificarea unei astfel de funcţii fractale. Profesorul Barnsley, care în trecut a predat la Georgia Institute of Technology a bebeficiat de fonduri guvernamentale de câteva milioane de dolari doar pentru a cerceta aceste tehnici de compresie a imaginilor. O aplicaţie militară importantă este transmiterea în timp real, prin satelit, a unor imagini cu un grad de detaliu mare.
Pentru a înţelege mai bine rolul computerelor în generarea fractalilor şi în aplicaţiile legate de aceştia vă voi expune modalitatea care se aplica în tehnica de compresie a imaginilor prin găsirea unei funcţii fractale care să poată fi folosită pentru micşorarea acestora înainte de inventarea unei modalităţi prin care computerele să poată să determine singure aceste funcţii. Sute de ore de muncă erau necesare pentru identificarea unei astfel de funcţii fractale. Profesorul Barnsley, care în trecut a predat la Georgia Institute of Technology a bebeficiat de fonduri guvernamentale de câteva milioane de dolari doar pentru a cerceta aceste tehnici de compresie a imaginilor. O aplicaţie militară importantă este transmiterea în timp real, prin satelit, a unor imagini cu un grad de detaliu mare.
Antena Fractală
Una dintre cele mai utile invenţii ce folosesc fractalii ca punct de plecare este antena fractală. Acest tip de antenă este construit după un tipar fractal (prin îndoirea sau modelarea unui volum sau prin găurire). Aceste antene sunt bazate pe forme fractale precum triunghiul lui Sierpinski, setul Mandelbrot, curba Koch sau insula Koch. Avantajele unei FEA (fractal element antenna) sunt reprezentate de mărimea redusă şi de lărgimea de bandă impresionantă. Mărimea poate fi redusă de două până la patru ori, obţinându-se performanţe remarcabile. Teoria funcţionării unei antene fractale îşi are originile în matematică, dar în cea mai simplă formă, această teorie se poate rezuma astfel: pentru ca o antenă să funcţioneze la fel de eficient pe toate frecvenţele, ea trebuie să satisfacă două condiţii; trebuie să fie simetrică faţă de un punct şi trebuie să posede o dimensiune de auto asemănare, adică să arate aproximativ la fel la orice scară. Aşadar, pe scurt, această antenă trebuie să fie fractală. În multe cazuri, folosirea unei antene fractale poate simplifica design- ul unui circuit, poate reduce costurile de construcţie şi poate conferi o mai mare siguranţă.
Haosul, definit ca o stare de dezorganizare, un amestec confuz şi dezorganizat de elemente, reprezintă mai nou o dezordine doar aparentă, rezultată din interacţiunea unor sisteme dinamice complexe ale căror reguli deabia acum încep să ni se dezvăluie. Cu ajutorul teoriei haosului pot fi explicate o serie de fenomene aparent întâmplătoare, care nu urmează regulile newtoniene în desfăşurare şi care prin nota puternică de hazard devin derutante. Cel mai interesant este însă modul în care această fizică a haosului poate fi implementată in viaţa de zi cu zi. Imaginaţi-vă că aţi putea explora evoluţia fenomenelor meteorologice, izbucnirea neprevăzută a epidemiilor, turbulenţa fluidelor şi chiar aritmiile inimii umane în secundele care precedă moartea fizică.Fractalii (scheme copiate de o infinitate de ori într-un spaţiu finit) pot fi priviţi ca o parte a haosului, deoarece se comportă la fel ca şi acesta din urmă. Ei prezintă un grad uimitor de complexitate şi chiar şi formulele de creare sunt asemănătoare. Legătura dintre fractali şi haos poate fi descrisă astfel : “ Orice mişcare haotică poate fi descrisă printr-o structură fractală şi elementele unui fractal sunt aşezate în plan în ordine haotică”.
Un fractal poate fi ilustrat prin două procedee. Unul dintre aceste procedee presupune folosirea culorilor pentru a ilustra cât de repede un anumit punct din planul complex tinde la infinit. Culorile pot fi alese aleatoriu, ele neinfluenţând în mod covârşitor modul de vizualizare a unui fractal. De fapt ,culorile pot fi înlocuite de o reprezentare 3D (se alege o dimensiune adiţională). Culorile dau impresia de mişcare, dar de fapt atunci când mărim sau micşorăm un fractal , acesta rămâne static, lucru şi logic de altfel, având în vedere că fractalul este la origine un sistem de puncte, iar aceste puncte au o poziţie bine determinată în planul complex. Sintagma “culori ale infinitului” nu ilustrează altceva decât modul în care culorile se schimbă pentru a evidenţia gradul infinit de detaliu al unui fractal (cu alte cuvinte, complexitatea infinită a lumii fractale).
Fractalii şi dimensiunea universului
Fractalii ar putea oferi în viitor răspunsul la câteva dintre întrebările ce tulbură umanitatea de mai multe secole. Cât de mare este universul şi dacă este cu adevărat infinit ? Stephen Hawking, fizician de renume, autor al lucrării “O scurtă istorie a timpului” şi profesor la Cambridge University, consideră că universul are dimensiuni limitate, cel putin la o scară inferioară. Această dimensiune limită se numeşte dimensiunea lui Planck (Planck length) şi are dimensiuni de ordinul a 10-24 inch.
Alţi oameni de ştiinţă opinează totuşi că universul ar fi infinit, el asemănându-se cu un fractal, ce are un grad infinit de complexitate, chiar dacă este puternic mărit. De altfel, Stephen Hawking este convins că universul poate fi descris cu ajutorul unor legi relativ simple, care însă nu au fost descoperite încă.
Alţi oameni de ştiinţă opinează totuşi că universul ar fi infinit, el asemănându-se cu un fractal, ce are un grad infinit de complexitate, chiar dacă este puternic mărit. De altfel, Stephen Hawking este convins că universul poate fi descris cu ajutorul unor legi relativ simple, care însă nu au fost descoperite încă.